Abrikosov vortex

In superconductivity, an Abrikosov vortex is a vortex of supercurrent in a type-II superconductor. The supercurrent circulates around the normal (i.e. non-superconducting) core of the vortex. The core has a size 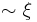$\sim\xi$ — the superconducting coherence length (parameter of a Ginzburg-Landau theory). The supercurrents decay on the distance about $\lambda$ (London penetration depth) from the core. 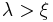Note that in type-II superconductors $\lambda>\xi$ . The circulating supercurrents induce magnetic fields with the total flux equal to a single flux quantum 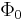$\Phi_0$ . Therefore, an Abrikosov vortex is often called a fluxon.

The magnetic field distribution of a single vortex far from its core can be described by

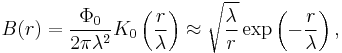
$B(r) = \frac{\Phi_0}{2\pi\lambda^2}K_0\left(\frac{r}{\lambda}\right) \approx \sqrt{\frac{\lambda}{r}} \exp\left(-\frac{r}{\lambda}\right),$

where 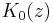$K_0(z)$ is a zeroth-order Bessel function. Note that, according to the above formula, at 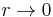$r \to 0$ the magnetic field 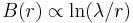$B(r)\propto\ln(\lambda/r)$ , i.e. logarithmically diverges. In reality, for 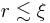$r\lesssim\xi$ the field is simply given by

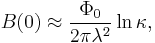
$B(0)\approx \frac{\Phi_0}{2\pi\lambda^2}\ln\kappa,$

where κ = λ/ξ is known as the Ginzburg-Landau parameter, which must be 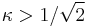$\kappa>1/\sqrt{2}$ in type-II superconductors.

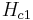Abrikosov vortices can be trapped in a type-II superconductor by chance, on defects, etc. Even if initially type-II superconductor contains no vortices, and one applies a magnetic field $H$ larger than the lower critical field $H_{c1}$ (but smaller than the upper critical field 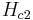$H_{c2}$ ), the field penetrates into superconductor in terms of Abrikosov vortices. Each vortex carries one thread of magnetic field with the flux 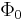$\Phi_0$ . Abrikosov vortices form a lattice (usually triangular, may be with defects/dislocations) with the average vortex density (flux density) approximately equal to the externally applied magnetic field.

Abrikosov vortex

See also